Page 18 - Ellingham, Mark, Mariusz Meszka, Primož Moravec, Enes Pasalic, 2014. 2014 PhD Summer School in Discrete Mathematics. Koper: University of Primorska Press. Famnit Lectures, 3.
P. 18
.1 Embeddings of graphs
Rotation schemes: If our surface is orientable and we know a consistent global clock-
wise orientation, we can describe the embedding just by giving the clockwise order
(rotation) of ends of edges at each vertex. This is a pure rotation system. Essentially
known by Heffter in 1891, formalized by Edmonds in 1960.
More general definition: If we do not know a consistent global clockwise orientation
(always true if our surface is nonorientable, but surface could also be orientable)
then we use a local clockwise orientation for each vertex to give the order of ends of
edges. But then we need to say whether rotations at two ends of an edge match up.
An edge is type 0 or signature 1 or untwisted if the local clockwise rotation of the vertex at
one end can be followed along the edge and agrees with the local clockwise rotation
of the vertex at the other end. Otherwise the edge is type 1 or signature −1 or twisted.
A rotation scheme in general consists of the orders of ends of edges around each vertex
plus the type of each edge. This is a purely combinatorial description.
We can tell if a closed walk in a graph is 1-sided from this. A walk is 1-sided if and only if
it contains an odd number of twisted (type 1) edges.
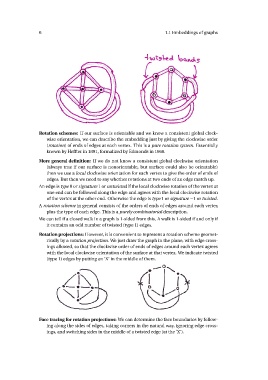
Rotation projections: However, it is convenient to represent a rotation scheme geomet-
rically by a rotation projection. We just draw the graph in the plane, with edge cross-
ings allowed, so that the clockwise order of ends of edges around each vertex agrees
with the local clockwise orientation of the surface at that vertex. We indicate twisted
(type 1) edges by putting an ‘X’ in the middle of them.
Face tracing for rotation projections: We can determine the face boundaries by follow-
ing along the sides of edges, taking corners in the natural way, ignoring edge cross-
ings, and switching sides in the middle of a twisted edge (at the ‘X’).
Rotation schemes: If our surface is orientable and we know a consistent global clock-
wise orientation, we can describe the embedding just by giving the clockwise order
(rotation) of ends of edges at each vertex. This is a pure rotation system. Essentially
known by Heffter in 1891, formalized by Edmonds in 1960.
More general definition: If we do not know a consistent global clockwise orientation
(always true if our surface is nonorientable, but surface could also be orientable)
then we use a local clockwise orientation for each vertex to give the order of ends of
edges. But then we need to say whether rotations at two ends of an edge match up.
An edge is type 0 or signature 1 or untwisted if the local clockwise rotation of the vertex at
one end can be followed along the edge and agrees with the local clockwise rotation
of the vertex at the other end. Otherwise the edge is type 1 or signature −1 or twisted.
A rotation scheme in general consists of the orders of ends of edges around each vertex
plus the type of each edge. This is a purely combinatorial description.
We can tell if a closed walk in a graph is 1-sided from this. A walk is 1-sided if and only if
it contains an odd number of twisted (type 1) edges.
Rotation projections: However, it is convenient to represent a rotation scheme geomet-
rically by a rotation projection. We just draw the graph in the plane, with edge cross-
ings allowed, so that the clockwise order of ends of edges around each vertex agrees
with the local clockwise orientation of the surface at that vertex. We indicate twisted
(type 1) edges by putting an ‘X’ in the middle of them.
Face tracing for rotation projections: We can determine the face boundaries by follow-
ing along the sides of edges, taking corners in the natural way, ignoring edge cross-
ings, and switching sides in the middle of a twisted edge (at the ‘X’).