Page 88 - Osnovne statistične metode in Jamovi

4 Statistična obdelava podatkov

 Izpis simbolov:

− Shapiro-Wilkov W označuje vrednost preizkusa Shapiro-Wilk, kar
označimo z oznako W.
− Shapiro-Wilkov p označuje pomembnost, kar označimo z oznako P ali
p.

 Primer razlage
Rezultat Shapiro-Wilkovega preizkusa za normalnost (W = 0,978; p < 0,001)
kaže, da se vrednost spremenljivke »Starost« ne porazdeljuje normalno.
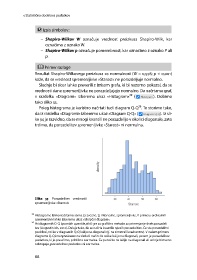
Slednje bi sicer lahko preverili z izrisom grafa, ki bi nazorno pokazal, da se
vrednosti dane spremenljivke ne porazdeljujejo normalno. Da načrtamo graf,
v razdelku »Diagrami« izberemo ukaz »Histogram«29 ( ). Dobimo
tako sliko 33.
Poleg histograma je koristno načrtati tudi diagram Q-Q30. To storimo tako,
da iz razdelka »Diagrami« izberemo ukaz »Diagram Q-Q« ( ). Iz sli-
ke 34 je razvidno, da se mnogi kvantili ne porazdelijo v okolici diagonale, zato
trdimo, da porazdelitev spremenljivke »Starost« ni normalna.

Slika 33 Porazdelitev vrednosti
spremenljivke »Starost«

29 Histograme lahko načrtamo samo za zvezne, tj. intervalne, spremenljivke. V primeru ordinalnih
spremenljivk lahko izberemo ukaz »Stolpčni diagram«.
30 Pri diagramih Q-Q (quantile-quantile plot) gre za grafično metodo za primerjanje dveh porazdeli-
tev (Augustin idr., 2012). Deluje tako, da se načrta kvantile njunih porazdelitev. Če sta porazdelitvi
podobni, točke v diagramih Q-Q ležijo na diagonali (tj. na simetrali kvadrantov). V našem primeru
diagrame Q-Q interpretiramo na sledeči način: če točke ležijo na diagonali, potem je porazdelitev
podatkov, ki jo preučimo, približno normalna. Če pa točke ne ležijo na diagonali ali od nje bistveno
odstopajo, porazdelitev podatkov ni normalna.

88