Page 32 - Ellingham, Mark, Mariusz Meszka, Primož Moravec, Enes Pasalic, 2014. 2014 PhD Summer School in Discrete Mathematics. Koper: University of Primorska Press. Famnit Lectures, 3.
P. 32
1.5 Transition graphs
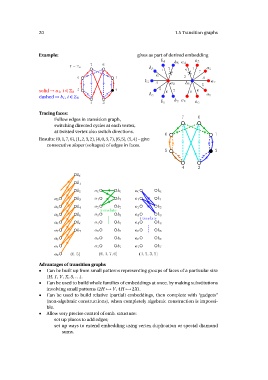
Example: gives as part of derived embedding
0 = Z8 7 0 b4 b5 a4 a5
6
b3 1 2 2 1 a7
7
1 0 3 4 a2
b7 4 a3 b6 5
solid → a i , i ∈ 8 5 2 b0 5 7 0 6 a1
6
dashed → bi , i ∈ 8 b1 b2 a6 a0
43
Tracing faces: 70
Follow edges in transition graph,
switching directed cycles at each vertex,
at twisted vertex also switch directions. 6 1
Results: (0, 1, 7, 6), (1, 2, 3, 2), (4, 0, 3, 7), (6, 5), (5, 4) – give
consecutive slopes (voltages) of edges in faces.
52
43
b0 a0 b0 a0 b0
b1 a1 b1 a1 b1
b2 a2 b2 a2 b2
a3 b3 a3 b3
a4 b4 translate
a5 b5 a3 b3 translate
a6 b6 a4 b4 a4 b4
a7 b7 a5 b5 a5 b5
a0 a6 b6 a6 b6
a1 a7 b7 a7 b7
a2 (6; 5)
(0; 1; 7; 6) (1; 2; 3; 2)
Advantages of transition graphs
• Can be built up from small patterns representing groups of faces of a particular size
(H , I , V , X , S, . . .).
• Can be used to build whole families of embeddings at once, by making substitutions
involving small patterns (2H ↔ V , 4H ↔ 2X ).
• Can be used to build relative (partial) embeddings, then complete with “gadgets”
(non-algebraic constructions), when completely algebraic construction is impossi-
ble.
• Allow very precise control of emb. structure:
set up places to add edges;
set up ways to extend embedding using vertex duplication or special diamond
sums.
Example: gives as part of derived embedding
0 = Z8 7 0 b4 b5 a4 a5
6
b3 1 2 2 1 a7
7
1 0 3 4 a2
b7 4 a3 b6 5
solid → a i , i ∈ 8 5 2 b0 5 7 0 6 a1
6
dashed → bi , i ∈ 8 b1 b2 a6 a0
43
Tracing faces: 70
Follow edges in transition graph,
switching directed cycles at each vertex,
at twisted vertex also switch directions. 6 1
Results: (0, 1, 7, 6), (1, 2, 3, 2), (4, 0, 3, 7), (6, 5), (5, 4) – give
consecutive slopes (voltages) of edges in faces.
52
43
b0 a0 b0 a0 b0
b1 a1 b1 a1 b1
b2 a2 b2 a2 b2
a3 b3 a3 b3
a4 b4 translate
a5 b5 a3 b3 translate
a6 b6 a4 b4 a4 b4
a7 b7 a5 b5 a5 b5
a0 a6 b6 a6 b6
a1 a7 b7 a7 b7
a2 (6; 5)
(0; 1; 7; 6) (1; 2; 3; 2)
Advantages of transition graphs
• Can be built up from small patterns representing groups of faces of a particular size
(H , I , V , X , S, . . .).
• Can be used to build whole families of embeddings at once, by making substitutions
involving small patterns (2H ↔ V , 4H ↔ 2X ).
• Can be used to build relative (partial) embeddings, then complete with “gadgets”
(non-algebraic constructions), when completely algebraic construction is impossi-
ble.
• Allow very precise control of emb. structure:
set up places to add edges;
set up ways to extend embedding using vertex duplication or special diamond
sums.