Page 33 - Ellingham, Mark, Mariusz Meszka, Primož Moravec, Enes Pasalic, 2014. 2014 PhD Summer School in Discrete Mathematics. Koper: University of Primorska Press. Famnit Lectures, 3.

k Ellingham: Construction Techniques for Graph Embeddings 21

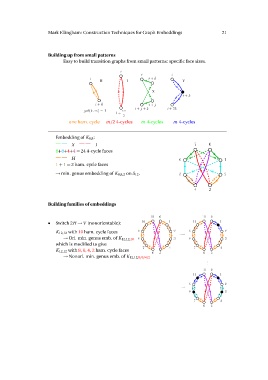
Building up from small patterns
Easy to build transition graphs from small patterns: specific face sizes.

i i i i

H I i+k V

X
i+k

i+k m i+j i + 2k
gcd(k; m) = 1 i+j +k
i+ m 4-cycles
2

one ham. cycle m /2 4-cycles m 4-cycles

Embedding of K8,8: 70
XI 61
52
8+8+4+4 = 24 4-cycle faces
H

1 + 1 = 2 ham. cycle faces

→ min. genus embedding of K8,8,2 on S12.

43

Building families of embeddings

• Switch 2H → V (nonorientable): 11 0 11 0 1
10 1 10 2
3
K12,12 with 10 ham. cycle faces 9 2 0! 9
4
→ Ori. min. genus emb. of K12,12,10 8 38
1
which is modified to give 47
65
K12,12 with 8, 6, 4, 2 ham. cycle faces 7
.
→ Nonori. min. genus emb. of K12,12,8/6/4/2 6 5 .
.
11 0
10

0! 9 2
3
8

74
65