Page 413 - Istenič Andreja, Gačnik Mateja, Horvat Barbara, Kukanja Gabrijelčič Mojca, Kiswarday Vanja Riccarda, Lebeničnik Maja, Mezgec Maja, Volk Marina. Ur. 2023. Vzgoja in izobraževanje med preteklostjo in prihodnostjo. Koper: Založba Univerze na Primorskem
P. 413
The Development of Strategies for Solving Arithmetic Word Problems
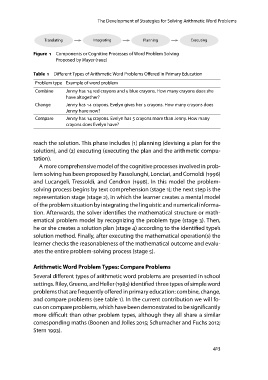
Translating Integrating Planning Executing
Figure 1 Components or Cognitive Processes of Word Problem Solving
Proposed by Mayer (1992)
Table 1 Different Types of Arithmetic Word Problems Offered in Primary Education
Problem type Example of word problem
Combine Jenny has red crayons and blue crayons. How many crayons does she
have altogether?
Change Jenny has crayons. Evelyn gives her crayons. How many crayons does
Jenny have now?
Compare Jenny has crayons. Evelyn has crayons more than Jenny. How many
crayons does Evelyn have?
reach the solution. This phase includes (1) planning (devising a plan for the
solution), and (2) executing (executing the plan and the arithmetic compu-
tation).
A more comprehensive model of the cognitive processes involved in prob-
lem solving has been proposed by Passolunghi, Lonciari, and Cornoldi (1996)
and Lucangeli, Tressoldi, and Cendron (1998). In this model the problem-
solving process begins by text comprehension (stage 1); the next step is the
representation stage (stage 2), in which the learner creates a mental model
of the problem situation by integrating the linguistic and numerical informa-
tion. Afterwards, the solver identifies the mathematical structure or math-
ematical problem model by recognizing the problem type (stage 3). Then,
he or she creates a solution plan (stage 4) according to the identified type’s
solution method. Finally, after executing the mathematical operation(s) the
learner checks the reasonableness of the mathematical outcome and evalu-
ates the entire problem-solving process (stage 5).
Arithmetic Word Problem Types: Compare Problems
Several different types of arithmetic word problems are presented in school
settings. Riley, Greeno, and Heller (1983) identified three types of simple word
problems that are frequently offered in primary education: combine, change,
and compare problems (see table 1). In the current contribution we will fo-
cus on compare problems, which have been demonstrated to be significantly
more difficult than other problem types, although they all share a similar
corresponding maths (Boonen and Jolles 2015; Schumacher and Fuchs 2012;
Stern 1993).
413
Translating Integrating Planning Executing
Figure 1 Components or Cognitive Processes of Word Problem Solving
Proposed by Mayer (1992)
Table 1 Different Types of Arithmetic Word Problems Offered in Primary Education
Problem type Example of word problem
Combine Jenny has red crayons and blue crayons. How many crayons does she
have altogether?
Change Jenny has crayons. Evelyn gives her crayons. How many crayons does
Jenny have now?
Compare Jenny has crayons. Evelyn has crayons more than Jenny. How many
crayons does Evelyn have?
reach the solution. This phase includes (1) planning (devising a plan for the
solution), and (2) executing (executing the plan and the arithmetic compu-
tation).
A more comprehensive model of the cognitive processes involved in prob-
lem solving has been proposed by Passolunghi, Lonciari, and Cornoldi (1996)
and Lucangeli, Tressoldi, and Cendron (1998). In this model the problem-
solving process begins by text comprehension (stage 1); the next step is the
representation stage (stage 2), in which the learner creates a mental model
of the problem situation by integrating the linguistic and numerical informa-
tion. Afterwards, the solver identifies the mathematical structure or math-
ematical problem model by recognizing the problem type (stage 3). Then,
he or she creates a solution plan (stage 4) according to the identified type’s
solution method. Finally, after executing the mathematical operation(s) the
learner checks the reasonableness of the mathematical outcome and evalu-
ates the entire problem-solving process (stage 5).
Arithmetic Word Problem Types: Compare Problems
Several different types of arithmetic word problems are presented in school
settings. Riley, Greeno, and Heller (1983) identified three types of simple word
problems that are frequently offered in primary education: combine, change,
and compare problems (see table 1). In the current contribution we will fo-
cus on compare problems, which have been demonstrated to be significantly
more difficult than other problem types, although they all share a similar
corresponding maths (Boonen and Jolles 2015; Schumacher and Fuchs 2012;
Stern 1993).
413