Page 479 - Istenič Andreja, Gačnik Mateja, Horvat Barbara, Kukanja Gabrijelčič Mojca, Kiswarday Vanja Riccarda, Lebeničnik Maja, Mezgec Maja, Volk Marina. Ur. 2023. Vzgoja in izobraževanje med preteklostjo in prihodnostjo. Koper: Založba Univerze na Primorskem
P. 479
The Equals Sign: The Challenges of Learning Arithmetic
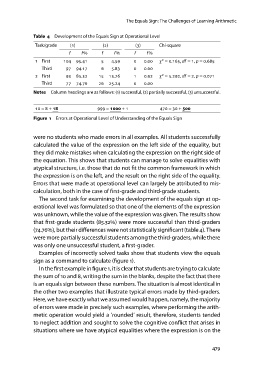
Table 4 Development of the Equals Sign at Operational Level
Task/grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . . χ2 = ., df = , p = .
Third . . .
. . .
First . . .
Third
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
= + = + = +
Figure 1 Errors at Operational Level of Understanding of the Equals Sign
were no students who made errors in all examples. All students successfully
calculated the value of the expression on the left side of the equality, but
they did make mistakes when calculating the expression on the right side of
the equation. This shows that students can manage to solve equalities with
atypical structure, i.e. those that do not fit the common framework in which
the expression is on the left, and the result on the right side of the equality.
Errors that were made at operational level can largely be attributed to mis-
calculation, both in the case of first-grade and third-grade students.
The second task for examining the development of the equals sign at op-
erational level was formulated so that one of the elements of the expression
was unknown, while the value of the expression was given. The results show
that first-grade students (85.32) were more successful than third-graders
(74.76), but their differences were not statistically significant (table 4). There
were more partially successful students among the third-graders, while there
was only one unsuccessful student, a first-grader.
Examples of incorrectly solved tasks show that students view the equals
sign as a command to calculate (figure 1).
In the first example in figure 1, it is clear that students are trying to calculate
the sum of 10 and 8, writing the sum in the blanks, despite the fact that there
is an equals sign between these numbers. The situation is almost identical in
the other two examples that illustrate typical errors made by third-graders.
Here, we have exactly what we assumed would happen, namely, the majority
of errors were made in precisely such examples, where performing the arith-
metic operation would yield a ‘rounded’ result, therefore, students tended
to neglect addition and sought to solve the cognitive conflict that arises in
situations where we have atypical equalities where the expression is on the
479
Table 4 Development of the Equals Sign at Operational Level
Task/grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . . χ2 = ., df = , p = .
Third . . .
. . .
First . . .
Third
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
= + = + = +
Figure 1 Errors at Operational Level of Understanding of the Equals Sign
were no students who made errors in all examples. All students successfully
calculated the value of the expression on the left side of the equality, but
they did make mistakes when calculating the expression on the right side of
the equation. This shows that students can manage to solve equalities with
atypical structure, i.e. those that do not fit the common framework in which
the expression is on the left, and the result on the right side of the equality.
Errors that were made at operational level can largely be attributed to mis-
calculation, both in the case of first-grade and third-grade students.
The second task for examining the development of the equals sign at op-
erational level was formulated so that one of the elements of the expression
was unknown, while the value of the expression was given. The results show
that first-grade students (85.32) were more successful than third-graders
(74.76), but their differences were not statistically significant (table 4). There
were more partially successful students among the third-graders, while there
was only one unsuccessful student, a first-grader.
Examples of incorrectly solved tasks show that students view the equals
sign as a command to calculate (figure 1).
In the first example in figure 1, it is clear that students are trying to calculate
the sum of 10 and 8, writing the sum in the blanks, despite the fact that there
is an equals sign between these numbers. The situation is almost identical in
the other two examples that illustrate typical errors made by third-graders.
Here, we have exactly what we assumed would happen, namely, the majority
of errors were made in precisely such examples, where performing the arith-
metic operation would yield a ‘rounded’ result, therefore, students tended
to neglect addition and sought to solve the cognitive conflict that arises in
situations where we have atypical equalities where the expression is on the
479