Page 483 - Istenič Andreja, Gačnik Mateja, Horvat Barbara, Kukanja Gabrijelčič Mojca, Kiswarday Vanja Riccarda, Lebeničnik Maja, Mezgec Maja, Volk Marina. Ur. 2023. Vzgoja in izobraževanje med preteklostjo in prihodnostjo. Koper: Založba Univerze na Primorskem
P. 483
The Equals Sign: The Challenges of Learning Arithmetic
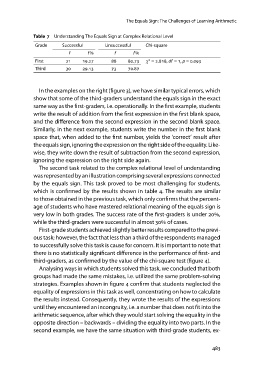
Table 7 Understanding The Equals Sign at Complex Relational Level
Grade Successful Unsuccessful Chi-square
f f f f χ2 = ., df = , p = .
First
Third . .
. .
In the examples on the right (figure 3), we have similar typical errors, which
show that some of the third-graders understand the equals sign in the exact
same way as the first-graders, i.e. operationally. In the first example, students
write the result of addition from the first expression in the first blank space,
and the difference from the second expression in the second blank space.
Similarly, in the next example, students write the number in the first blank
space that, when added to the first number, yields the ‘correct’ result after
the equals sign, ignoring the expression on the right side of the equality. Like-
wise, they write down the result of subtraction from the second expression,
ignoring the expression on the right side again.
The second task related to the complex relational level of understanding
was represented by an illustration comprising several expressions connected
by the equals sign. This task proved to be most challenging for students,
which is confirmed by the results shown in table 4. The results are similar
to those obtained in the previous task, which only confirms that the percent-
age of students who have mastered relational meaning of the equals sign is
very low in both grades. The success rate of the first-graders is under 20,
while the third-graders were successful in almost 30 of cases.
First-grade students achieved slightly better results compared to the previ-
ous task; however, the fact that less than a third of the respondents managed
to successfully solve this task is cause for concern. It is important to note that
there is no statistically significant difference in the performance of first- and
third-graders, as confirmed by the value of the chi-square test (figure 4).
Analysing ways in which students solved this task, we concluded that both
groups had made the same mistakes, i.e. utilized the same problem-solving
strategies. Examples shown in figure 4 confirm that students neglected the
equality of expressions in this task as well, concentrating on how to calculate
the results instead. Consequently, they wrote the results of the expressions
until they encountered an incongruity, i.e. a number that does not fit into the
arithmetic sequence, after which they would start solving the equality in the
opposite direction – backwards – dividing the equality into two parts. In the
second example, we have the same situation with third-grade students, ex-
483
Table 7 Understanding The Equals Sign at Complex Relational Level
Grade Successful Unsuccessful Chi-square
f f f f χ2 = ., df = , p = .
First
Third . .
. .
In the examples on the right (figure 3), we have similar typical errors, which
show that some of the third-graders understand the equals sign in the exact
same way as the first-graders, i.e. operationally. In the first example, students
write the result of addition from the first expression in the first blank space,
and the difference from the second expression in the second blank space.
Similarly, in the next example, students write the number in the first blank
space that, when added to the first number, yields the ‘correct’ result after
the equals sign, ignoring the expression on the right side of the equality. Like-
wise, they write down the result of subtraction from the second expression,
ignoring the expression on the right side again.
The second task related to the complex relational level of understanding
was represented by an illustration comprising several expressions connected
by the equals sign. This task proved to be most challenging for students,
which is confirmed by the results shown in table 4. The results are similar
to those obtained in the previous task, which only confirms that the percent-
age of students who have mastered relational meaning of the equals sign is
very low in both grades. The success rate of the first-graders is under 20,
while the third-graders were successful in almost 30 of cases.
First-grade students achieved slightly better results compared to the previ-
ous task; however, the fact that less than a third of the respondents managed
to successfully solve this task is cause for concern. It is important to note that
there is no statistically significant difference in the performance of first- and
third-graders, as confirmed by the value of the chi-square test (figure 4).
Analysing ways in which students solved this task, we concluded that both
groups had made the same mistakes, i.e. utilized the same problem-solving
strategies. Examples shown in figure 4 confirm that students neglected the
equality of expressions in this task as well, concentrating on how to calculate
the results instead. Consequently, they wrote the results of the expressions
until they encountered an incongruity, i.e. a number that does not fit into the
arithmetic sequence, after which they would start solving the equality in the
opposite direction – backwards – dividing the equality into two parts. In the
second example, we have the same situation with third-grade students, ex-
483