Page 480 - Istenič Andreja, Gačnik Mateja, Horvat Barbara, Kukanja Gabrijelčič Mojca, Kiswarday Vanja Riccarda, Lebeničnik Maja, Mezgec Maja, Volk Marina. Ur. 2023. Vzgoja in izobraževanje med preteklostjo in prihodnostjo. Koper: Založba Univerze na Primorskem
P. 480
ja Maričić, Nenad Milinković, and Marija Brković
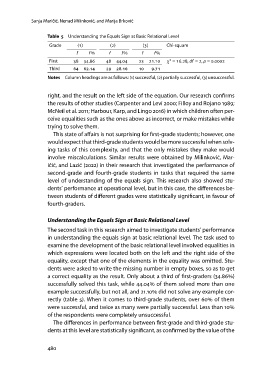
Table 5 Understanding the Equals Sign at Basic Relational Level
Grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . .
Third . . .
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
right, and the result on the left side of the equation. Our research confirms
the results of other studies (Carpenter and Levi 2000; Filloy and Rojano 1989;
McNeil et al. 2011; Harbour, Karp, and Lingo 2016) in which children often per-
ceive equalities such as the ones above as incorrect, or make mistakes while
trying to solve them.
This state of affairs is not surprising for first-grade students; however, one
would expect that third-grade students would be more successful when solv-
ing tasks of this complexity, and that the only mistakes they make would
involve miscalculations. Similar results were obtained by Milinković, Mar-
ičić, and Lazić (2022) in their research that investigated the performance of
second-grade and fourth-grade students in tasks that required the same
level of understanding of the equals sign. This research also showed stu-
dents’ performance at operational level, but in this case, the differences be-
tween students of different grades were statistically significant, in favour of
fourth-graders.
Understanding the Equals Sign at Basic Relational Level
The second task in this research aimed to investigate students’ performance
in understanding the equals sign at basic relational level. The task used to
examine the development of the basic relational level involved equalities in
which expressions were located both on the left and the right side of the
equality, except that one of the elements in the equality was omitted. Stu-
dents were asked to write the missing number in empty boxes, so as to get
a correct equality as the result. Only about a third of first-graders (34.86)
successfully solved this task, while 44.04 of them solved more than one
example successfully, but not all, and 21.10 did not solve any example cor-
rectly (table 5). When it comes to third-grade students, over 60 of them
were successful, and twice as many were partially successful. Less than 10
of the respondents were completely unsuccessful.
The differences in performance between first-grade and third-grade stu-
dents at this level are statistically significant, as confirmed by the value of the
480
Table 5 Understanding the Equals Sign at Basic Relational Level
Grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . .
Third . . .
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
right, and the result on the left side of the equation. Our research confirms
the results of other studies (Carpenter and Levi 2000; Filloy and Rojano 1989;
McNeil et al. 2011; Harbour, Karp, and Lingo 2016) in which children often per-
ceive equalities such as the ones above as incorrect, or make mistakes while
trying to solve them.
This state of affairs is not surprising for first-grade students; however, one
would expect that third-grade students would be more successful when solv-
ing tasks of this complexity, and that the only mistakes they make would
involve miscalculations. Similar results were obtained by Milinković, Mar-
ičić, and Lazić (2022) in their research that investigated the performance of
second-grade and fourth-grade students in tasks that required the same
level of understanding of the equals sign. This research also showed stu-
dents’ performance at operational level, but in this case, the differences be-
tween students of different grades were statistically significant, in favour of
fourth-graders.
Understanding the Equals Sign at Basic Relational Level
The second task in this research aimed to investigate students’ performance
in understanding the equals sign at basic relational level. The task used to
examine the development of the basic relational level involved equalities in
which expressions were located both on the left and the right side of the
equality, except that one of the elements in the equality was omitted. Stu-
dents were asked to write the missing number in empty boxes, so as to get
a correct equality as the result. Only about a third of first-graders (34.86)
successfully solved this task, while 44.04 of them solved more than one
example successfully, but not all, and 21.10 did not solve any example cor-
rectly (table 5). When it comes to third-grade students, over 60 of them
were successful, and twice as many were partially successful. Less than 10
of the respondents were completely unsuccessful.
The differences in performance between first-grade and third-grade stu-
dents at this level are statistically significant, as confirmed by the value of the
480