Page 482 - Istenič Andreja, Gačnik Mateja, Horvat Barbara, Kukanja Gabrijelčič Mojca, Kiswarday Vanja Riccarda, Lebeničnik Maja, Mezgec Maja, Volk Marina. Ur. 2023. Vzgoja in izobraževanje med preteklostjo in prihodnostjo. Koper: Založba Univerze na Primorskem
P. 482
ja Maričić, Nenad Milinković, and Marija Brković
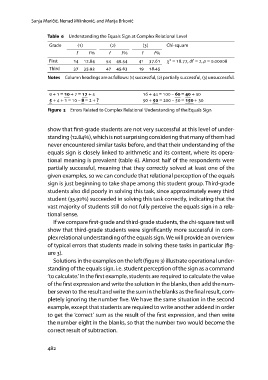
Table 6 Understanding the Equals Sign at Complex Relational Level
Grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . .
Third . . .
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
+ = + = + + = – = +
+ + = – = + ? + = – = +
Figure 3 Errors Related to Complex Relational Understanding of the Equals Sign
show that first-grade students are not very successful at this level of under-
standing (12.84), which is not surprising considering that many of them had
never encountered similar tasks before, and that their understanding of the
equals sign is closely linked to arithmetic and its content, where its opera-
tional meaning is prevalent (table 6). Almost half of the respondents were
partially successful, meaning that they correctly solved at least one of the
given examples, so we can conclude that relational perception of the equals
sign is just beginning to take shape among this student group. Third-grade
students also did poorly in solving this task, since approximately every third
student (35.92) succeeded in solving this task correctly, indicating that the
vast majority of students still do not fully perceive the equals sign in a rela-
tional sense.
If we compare first-grade and third-grade students, the chi-square test will
show that third-grade students were significantly more successful in com-
plex relational understanding of the equals sign. We will provide an overview
of typical errors that students made in solving these tasks in particular (fig-
ure 3).
Solutions in the examples on the left (figure 3) illustrate operational under-
standing of the equals sign, i.e. student perception of the sign as a command
‘to calculate.’ In the first example, students are required to calculate the value
of the first expression and write the solution in the blanks, then add the num-
ber seven to the result and write the sum in the blanks as the final result, com-
pletely ignoring the number five. We have the same situation in the second
example, except that students are required to write another addend in order
to get the ‘correct’ sum as the result of the first expression, and then write
the number eight in the blanks, so that the number two would become the
correct result of subtraction.
482
Table 6 Understanding the Equals Sign at Complex Relational Level
Grade () () () Chi-square
f f f f f f χ2 = ., df = , p = .
First . . .
Third . . .
Notes Column headings are as follows: (1) successful, (2) partially successful, (3) unsuccessful.
+ = + = + + = – = +
+ + = – = + ? + = – = +
Figure 3 Errors Related to Complex Relational Understanding of the Equals Sign
show that first-grade students are not very successful at this level of under-
standing (12.84), which is not surprising considering that many of them had
never encountered similar tasks before, and that their understanding of the
equals sign is closely linked to arithmetic and its content, where its opera-
tional meaning is prevalent (table 6). Almost half of the respondents were
partially successful, meaning that they correctly solved at least one of the
given examples, so we can conclude that relational perception of the equals
sign is just beginning to take shape among this student group. Third-grade
students also did poorly in solving this task, since approximately every third
student (35.92) succeeded in solving this task correctly, indicating that the
vast majority of students still do not fully perceive the equals sign in a rela-
tional sense.
If we compare first-grade and third-grade students, the chi-square test will
show that third-grade students were significantly more successful in com-
plex relational understanding of the equals sign. We will provide an overview
of typical errors that students made in solving these tasks in particular (fig-
ure 3).
Solutions in the examples on the left (figure 3) illustrate operational under-
standing of the equals sign, i.e. student perception of the sign as a command
‘to calculate.’ In the first example, students are required to calculate the value
of the first expression and write the solution in the blanks, then add the num-
ber seven to the result and write the sum in the blanks as the final result, com-
pletely ignoring the number five. We have the same situation in the second
example, except that students are required to write another addend in order
to get the ‘correct’ sum as the result of the first expression, and then write
the number eight in the blanks, so that the number two would become the
correct result of subtraction.
482