Page 121 - Osnovne statistične metode in Jamovi

4.3 Parametrični preizkusi

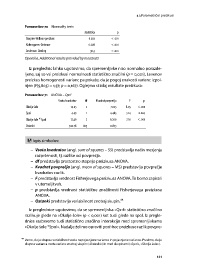
Ponazoritev 70 Normality tests
statistika p
Shapiro-Wilksov preizkus 0.922 < .001
Kolmogorov-Smirnov 0.208 < .001
Anderson-Darling 30.3 < .001

Opomba. Additional results provided by moretests

Iz preglednic lahko ugotovimo, da spremenljivke niso normalno porazde-
ljene, saj so vsi preizkusi normalnosti statistično značilni (p = 0,001), Levenov
preizkus homogenosti varianc pa pokaže, da je pogoj enakosti varianc izpol-
njen (F(5,803) = 1,57; p = 0,167). Oglejmo si zdaj rezultate preizkusa:

Ponazoritev 71 ANOVA – Q21f
Vsota kvadratov df Kvadrat povprečja F p
Okolje šole 14.05 2 7.025 8.05 < .001
Spol 4.49 1 4.485 5.14 0.024
Okolje šole * Spol 12.40 2 6.200 7.10 < .001
Ostanki 700.78 803 0.873

 Izpis simbolov:

− Vsota kvadratov (angl. sum of squares – SS) predstavlja način merjenja
razpršenosti, tj. razlike od povprečja.
− df predstavlja prostostno stopnjo preizkusa ANOVA.
− Kvadrat povprečja (angl. mean of squares – MS) predstavlja povprečje
kvadratov razlik.
− F predstavlja vrednost Fisherjevega preizkusa ANOVA. To bomo zapisali
v utemeljitvah.
− p predstavlja vrednost statistične značilnosti Fisherjevega preizkusa
ANOVA.
− Ostanki predstavlja variabilnost znotraj skupin.48

Iz preglednice ugotovimo, da se spremenljivka »Q21f« statistično značilno
razlikuje glede na »Okolje šole« (p < 0,001) kot tudi glede na spol. Iz pregle-
dnice razberemo tudi statistično značilno interakcijo med spremenljivkama
»Okolje šole *Spol«. Nadalje želimo opraviti post-hoc preizkuse razlik povpre-

48 Vemo, da je skupna variabilnost vsota nepojasnjene variance in pojasnjene variance. Pravimo, da je
skupna varianca vsota varianc znotraj skupin (»Ostanki«) in med skupinami (»Spol«, »Okolje šole«).

121