Page 566 - Pedagoška vizija / A Pedagogical Vision

Mara Cotič, Daniel Doz, Matija Jenko in Amalija Žakelj

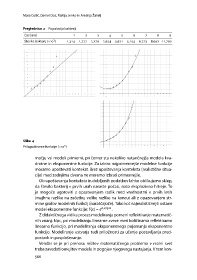
Preglednica 2 Populacija bakterij
Čas (ure)         
3
Število bakterij (×10 ) , , ,, , , , , ,

Slika 4
3
Prilagoditvene funkcije (×10 )
močju vsi modeli primerni, pri čemer sta nekoliko natančnejša modela kva-
dratne in eksponentne funkcije. Za izbiro najprimernejše modelne funkcije
moramo upoštevati kontekst. Brez upoštevanja konteksta (realistične situa-
cije) med zadnjima dvema ne moremo izbrati primernejše.
Ob upoštevanju konteksta in dobljenih podatkov lahko oblikujemo sklep,
da število bakterij v prvih urah naraste počasi, nato eksplozivno hitreje. To
je mogoče ugotoviti z opazovanjem razlik med vrednostmi v prvih letih
(majhne razlike na začetku, velike razlike na koncu) ali z opazovanjem str-
mine grafov modelnih funkcij (naraščajoče). Tako kot najrealističnejši ostane
model eksponentne funkcije: f(x) = e 0,2732x .
Z didaktičnega vidika proces modeliranja pomeni reflektiranje matematič-
nih znanj. Npr., pri modeliranju linearne zveze med količinama reflektiramo
linearno funkcijo, pri modeliranju eksponentnega pojemanja eksponentno
funkcijo. Modeliranje ustvarja tudi priložnosti za učenje postavljanja pred-
postavk in posploševanja.
Vendar se je pri prenosu rešitev matematičnega problema v realni svet
treba zavedati omejitev modela in pogojev njegovega nastajanja. V tem kon-
566